My son and I were playing the card game “Set” this weekend. It’s a fun pattern matching game, and if you don’t know the rules, they’re available online here. Basically you deal out 12 cards and look for a set of 3 cards that fit a certain pattern. Each time a set is removed, 3 more cards are dealt to return the number of face up cards to 12. As each set is removed, this happens 23 times until the remaining 69 cards are gone. The winner is the person who has discovered the most sets.
In the instructions it says that there are 33:1 odds of having a set that fits the criteria when 12 cards are face up, and about 2500:1 when 15 cards are face up. In this one game, we kept being unable to find a set among 12 cards. When this happened we dealt another 3 cards (to make 15) and were usually able to find a set right away. But we were definitely getting stuck more than 1 in 34 times.
I wanted to find out what is the probability of having a set among 12 cards (and 15 for that matter). To do this, of course, I turned to R.
Create the Deck
Each card has 4 attributes, each of which has 3 different variations. I represented each attribute as a1, a2, a3, or a4, and each variation as 0, 1, or 2.
library(tictoc)
a1 <- rep(c(0,1,2), rep(27, 3))
a2 <- rep(rep(c(0,1,2), rep(9, 3)), 3)
a3 <- rep(rep(c(0,1,2), rep(3, 3)), 9)
a4 <- rep(c(0,1,2), 27)
cards <- data.frame(a1, a2, a3, a4)Combinations of 3 Cards
# number of 3 card combinations in deck
81*80*79/3/2## [1] 85320# number of 3 card combinations in 12 cards
12*11*10/3/2## [1] 220Testing if 3 Cards are a Set
To test if 3 cards are a set, I sampled 3 card numbers at random by choosing 3 integers between 1 and 82 inclusive. Then I extracted the cards’ attributes for those cards and summed them.
Here’s a little more about the game. In order for 3 cards to meet the set criteria, each attribute must be the same for all 3 cards, or different for all 3 cards. So a1 has to be all 0s or all 1s or all 2s or 0, 1, and 2. Attribute 2 doesn’t have to follow the same pattern as a1, just all the same or all different. Same for a3 and a4…
So if we sum the attributes, they have to be equal to 0+0+0=0 or 1+1+1=3 or 2+2+2=6, or 0+1+2=3. Again, they can only be 0, 3, or 6. If we have 0+1+0, that’s not right. Or 0+2+2, again not right. There is no other way to make 0, 3, or 6 other than by them all to be the same or all to be different.
Mathematics Aside: Given 3 Random Cards, What Is the Probability They Are a Set?
This hints at the calculation that would need to be done to do this in a mathematics way. For an attribute, each card can have 3 outcomes (0, 1, 2). There are 27 possible permutations, and 3 possible ways for them to be all the same and 6 possible ways for them to be all different. So for each attribute there is a 9/27, or 1/3, chance that it meets the criteria. Given random distribution of the attributes, for each of 4 attributes to meet the criteria, we would calculate that probability as (1/3)^4 or 1/81, or about 1.2%.
When you deal 12 cards, there are 220 combinations of 3. They are not all independent since many of them have the same card within them. I have to do some more thinking about how the dependence affects the probability of finding at least one set that meets the criteria, but apparently this increases the probability of finding a set.
Back to the Programming
Ok, now back to the programming. We take 3 cards, sum their attributes, and then see if each attribute’s sum is equal to 0, 3, or 6. If they are all equal to 0, 3, or 6, then they are a set! Below I set up some functions to test if a trio of cards is a set.
set.seed(1)
trio <- cards[sample(1:81, 3), ]
trio # cards' attributes## a1 a2 a3 a4
## 68 2 1 1 1
## 39 1 1 0 2
## 1 0 0 0 0colSums(trio) # sum the attributes## a1 a2 a3 a4
## 3 2 1 3trio_sum <- colSums(trio)
# Helper function that tests whether a number is 0, 3, or 6.
test1 <- function(x) x %in% c(0, 3, 6)
sapply(trio_sum, test1) # test if each individual attribute meets the set condition## a1 a2 a3 a4
## TRUE FALSE FALSE TRUEall(sapply(trio_sum, test1)) # test if all attributes meet the set condition## [1] FALSEprod(sapply(trio_sum, test1)) # alternate test if all attributes are true## [1] 0# Helper function that tests whether 3 cards' attributes are a set
is_set <- function(trio) all(sapply(colSums(trio), test1))
is_set(trio)## [1] FALSE# Test if function returns true for the following sets
is_set(matrix(rep(0, 12), 3)) # all 0## [1] TRUEis_set(matrix(rep(1, 12), 3)) # all 1## [1] TRUEis_set(matrix(rep(2, 12), 3)) # all 2## [1] TRUEis_set(matrix(rep(c(0,1,2), 4), 3)) # all 0, 1, and 2## [1] TRUESimulating Finding Sets in a Deal of 12 Cards
Now we can build a little closer to the game. First we draw 12 cards.
# Draw 12 cards
set.seed(1)
deal <- sample(1:81, 12)
deal # card numbers## [1] 68 39 1 34 43 14 59 51 21 54 7 37Within those 12 cards, we need to find all combinations of 3 cards.
# Find all combinations of sets of 3
sets <- combn(deal, 3, simplify = F)
head(sets)## [[1]]
## [1] 68 39 1
##
## [[2]]
## [1] 68 39 34
##
## [[3]]
## [1] 68 39 43
##
## [[4]]
## [1] 68 39 14
##
## [[5]]
## [1] 68 39 59
##
## [[6]]
## [1] 68 39 51Since we’re just drawing card numbers, we have to back up the function a little more above to take the given card numbers, extract the attributes for those card numbers, then test if they form a set.
# Function that takes a set of 3 cards numbers and determines if their
# attributes form a true Set
test_set <- function(set) {
cards[set, ] |> is_set()
}We can apply the function to all the combinations in the cards dealt.
sapply(sets, test_set)## [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [13] FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE TRUE
## [25] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [37] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [49] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [61] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [73] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [85] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [97] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [109] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [121] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [133] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [145] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [157] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [169] FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [181] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [193] FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [205] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [217] FALSE FALSE FALSE FALSEIn this draw of 12 cards we find that there are actually 4 Sets!
table(sapply(sets, test_set))##
## FALSE TRUE
## 216 4The sets that fulfill the Set criteria are the following:
which(sapply(sets, test_set) == TRUE)## [1] 17 24 172 196The card numbers and their attributes in those sets are:
sets_true <- sets[which(sapply(sets, test_set) == TRUE)]
sets_true # which sets fulfill the Set criteria## [[1]]
## [1] 68 1 54
##
## [[2]]
## [1] 68 34 21
##
## [[3]]
## [1] 43 59 21
##
## [[4]]
## [1] 14 21 7# The actual card attributes are:
lapply(sets_true, function(x) cards[unlist(x),])## [[1]]
## a1 a2 a3 a4
## 68 2 1 1 1
## 1 0 0 0 0
## 54 1 2 2 2
##
## [[2]]
## a1 a2 a3 a4
## 68 2 1 1 1
## 34 1 0 2 0
## 21 0 2 0 2
##
## [[3]]
## a1 a2 a3 a4
## 43 1 1 2 0
## 59 2 0 1 1
## 21 0 2 0 2
##
## [[4]]
## a1 a2 a3 a4
## 14 0 1 1 1
## 21 0 2 0 2
## 7 0 0 2 0So we can see that the trios of cards actually look like sets…
Repeating the Simulation 1000 times
Ok now that we have shown that we can simulate the 12 cards, let’s simulate the probability that a random draw of 12 cards will contain at least one set.
To do this we need a function that takes as its input a vector of 12 card numbers and returns the number of sets found.
set_sim <- function(deal) {
sets <- combn(deal, 3, simplify = F)
sum(sapply(sets, test_set))
}Yikes, is that all that’s needed? Seems like too good to be true. Testing it on the original random deal from above gets the same answer. Ok then…
set_sim(deal) ## [1] 4Now let’s create 1000 random deals. Google tip to this link.
set.seed(1)
deals <- replicate(1000, sample(1:81,size=12), simplify=FALSE)
head(deals)## [[1]]
## [1] 68 39 1 34 43 14 59 51 21 54 7 37
##
## [[2]]
## [1] 37 34 44 33 35 70 74 42 38 20 28 72
##
## [[3]]
## [1] 44 70 40 81 25 80 39 51 42 6 24 32
##
## [[4]]
## [1] 14 2 45 18 22 65 70 75 13 40 48 23
##
## [[5]]
## [1] 29 13 22 28 48 33 45 21 31 17 77 64
##
## [[6]]
## [1] 60 51 34 10 1 43 59 26 15 58 29 24tic()
deals_sets <- sapply(deals, set_sim)
toc()## 30.512 sec elapsedtable(deals_sets)## deals_sets
## 0 1 2 3 4 5 6 7 8
## 34 165 253 270 174 78 20 5 1Ohhh… that took a while even with only 1000 samples and trying to use vector methods as much as I could. That being said, it produced a really nice distribution here!
hist(deals_sets)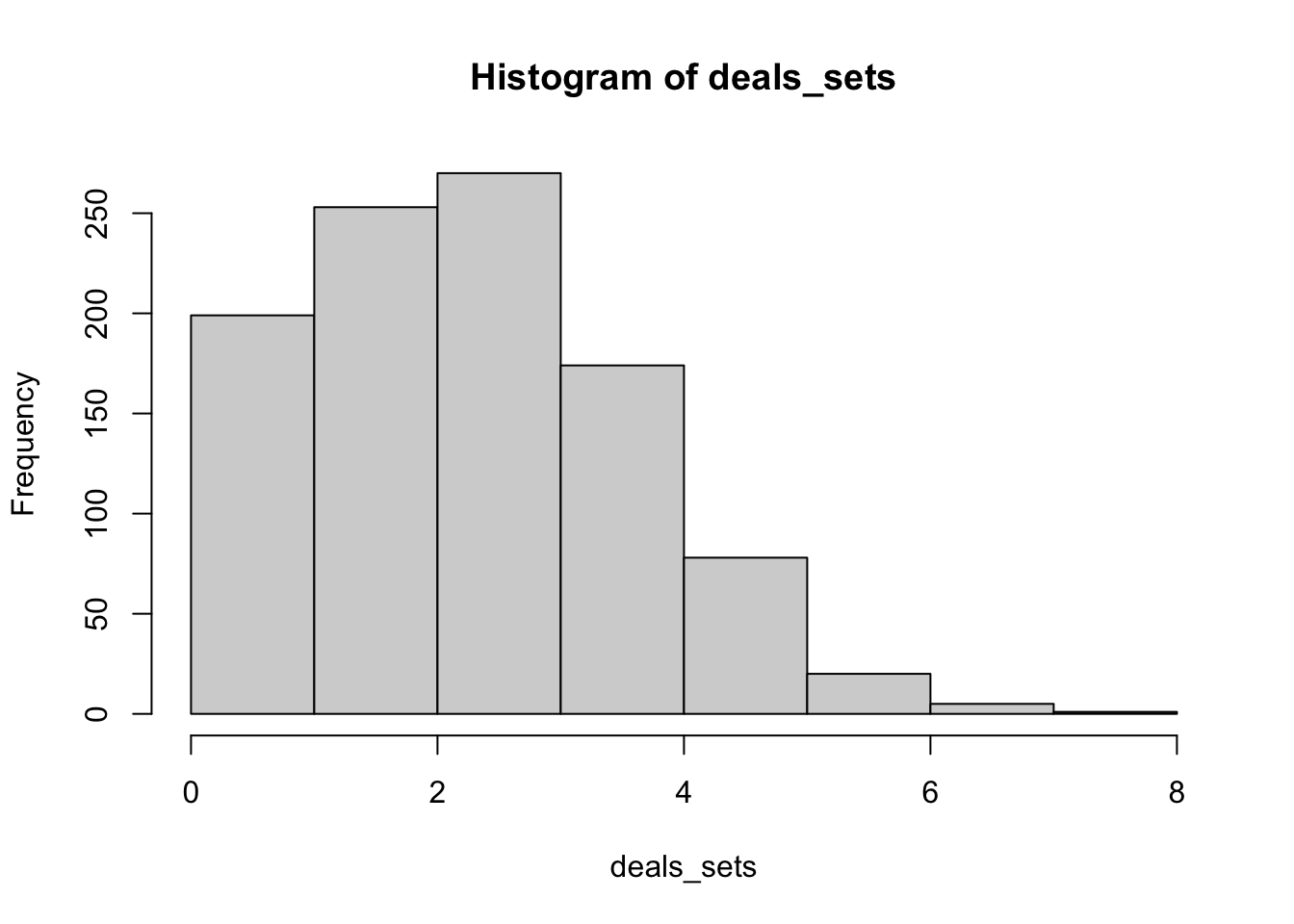
So out of 1000 random deals of 12 cards, 34 did not have any sets. That’s a 3.4% rate of not finding a set, or 96.6% rate of finding a set. This compares well to their cited 33:1 odds of finding a set, which of course, is 33/34 or 97%.
In addition, the most common number of sets is not 1, and not even 2. It’s 3 sets! Actually according to this simulation, there is a greater than 50% chance of there being 3 or more sets found among the 12 cards!
We can do the same thing for 15 cards, but we would probably have to run 10000 trials given that it says 2500:1 odds of finding a match. On my puny laptop, that might take all day!
set.seed(1)
deals <- replicate(30000, sample(1:81,size=15), simplify=FALSE)
head(deals)## [[1]]
## [1] 68 39 1 34 43 14 59 51 21 54 7 37 70 78 44
##
## [[2]]
## [1] 79 33 35 70 74 42 38 20 28 77 44 78 40 71 25
##
## [[3]]
## [1] 70 39 51 42 6 24 32 14 2 45 18 22 65 13 40
##
## [[4]]
## [1] 48 23 29 13 22 28 81 33 45 21 31 17 75 64 60
##
## [[5]]
## [1] 51 34 10 1 43 59 26 15 58 29 24 42 48 39 71
##
## [[6]]
## [1] 53 40 35 43 1 29 22 70 28 37 61 46 67 51 44tic()
deals_sets <- sapply(deals, set_sim)
toc()## 7860.368 sec elapsedtable(deals_sets)## deals_sets
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
## 11 144 792 2281 4410 6028 6247 4938 2995 1463 498 146 39 5 3hist(deals_sets)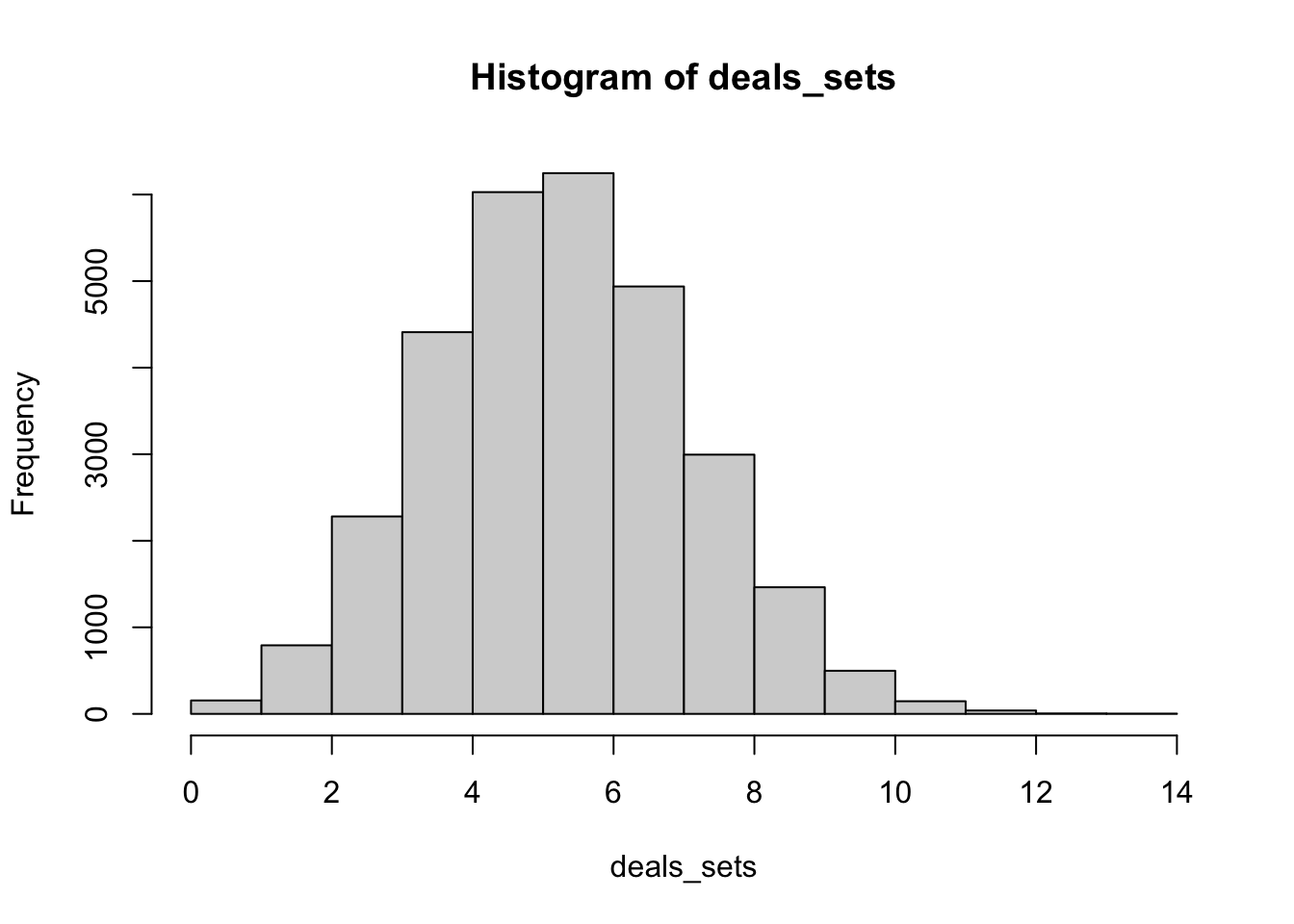
So I let that chunk above run while I went to work. It took 7860 seconds, or 2 hours 11 minutes on my puny laptop.
After 30,000 simulations of a 15 card deal, I found 11 where there were no sets. This is about 0.03% or 2727:1. That’s pretty close to what it says in the instruction book for the game, 2500:1.
deals_sets
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
11 144 792 2281 4410 6028 6247 4938 2995 1463 498 146 39 5 3 Notes
I had to figure some stuff out here because of updates to hugo and blogdown. Now blogdown doesn’t build the site so I had to manually call build_site(local = TRUE) to rebuild the Github pages directory, then push it to Github. Images were broken in preview but worked after pushing to Github. All in all, this method of publishing the blog is starting to become more kludgy, and it may be soon time to jump ship to Netlify!